Bei Bedarfszahlen mit einem trendförmigen Verlauf muss festgestellt
werden, ob die Zahlen um eine
Regressionskurven können mit einer Unsicherheit behaftet sein. Wie groß die
Genauigkeit der Kurve ist, wird durch die Vertrauensgrenze ausgedrückt,
deren
Berechnung aber einen hohen Rechenaufwand erfordert. Eine Gewichtung der Daten
ist nicht möglich.
Entsprechend dem betrachteten Kurvenverlauf werden unterschieden:

Bei einem linear verlaufenden Trend bietet es sich an, eine lineare Regressionsanalyse durchzuführen, für die es - als Trendrechnung - eine vereinfachte Form ergibt:
![]()
y = Regressionswert in Abhängigkeit von der Zeit
a = Die von der Regressionskurve auf der y-Achse abgeschnittene Größe
b = Regressionskoeffizient
t = Steigungsmaß der Regressionskurve
Die Werte a, b, t werden folgendermaßen ermittelt:
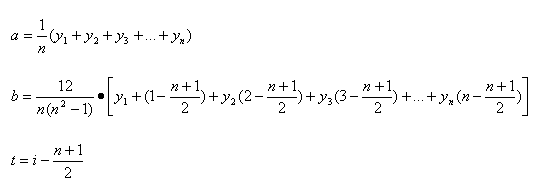
Es folgt die Berechnung eines Beispiels in einem Java Applet:
(Die Werte für Quartal 1 bis 4 (Q1 bis Q4) sind gegeben, die Werte für Quartal
5 und 6 (Q5 und Q6) werden berechnet.)
|
|
Die nicht lineare Regressionsanalyse findet ihre Anwendung bei nicht linearem Verlauf der Kurve des Materialbedarfes.
Für die nicht lineare Regressionsanalyse gilt:
![]()
Die nicht lineare Regressionsanalyse versucht über die
![]()
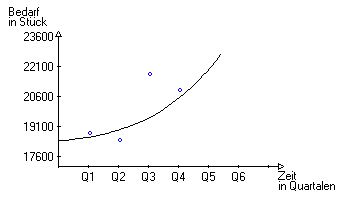
sich den nicht linearen Bedarfsverläufen anzupassen. Eine Anwendung ist nur bei Einsatz von EDV-Programmen möglich, wobei das Programm die Regressionskurve "selbständig" ermittelt. Diese Kurve kann folgendermaßen aussehen:
|